The Golden Ratio: Form, Size & Distance In Space

The Golden Proportion is the relationship of measurements that is considered perfect. Artists have used this proportion for ages because of its ideal beauty and interest. But the Golden Proportion is not just a mysterious number. It mathematically unites objects into a grid and clarifies to the mind an object’s mass and distance.

Mass and Distance Proportion & Form Determine Size Quantum Relationship

Very simple mathematics allows us to see how the Golden Mean relates multiple objects. Leonardo of Pisa used his Fibonacci sequence in 1202 A.D. to describe animal populations over time. He noticed that the overall population size was in direct proportion to the age at which the animals start to mate. If we consider a group of objects in physical space, we can therefore use this proportion to relate the overall size of the group and the distance between the individual objects. In nature, environments conform to this golden mean because it is the ideal size of objects within an overall group.

 

Linear Relationship of Mass & Distance   Imagine you are looking at two telephone poles on the skyline. You cannot tell how far away they are from you, but it looks like they are all the same size and distance from each other. Now, imagine you are looking at the telephone poles from a high up point of view. You realize that one of them is much farther away than the other one, but it is also much larger, so that made it look closer when you were on the ground. This optical illusion happens because both size and distance tell your eye if an object is far away or close to you. Something looks big if it is close, and it looks close if it is big. This simple fact provides the basis for relationships of all objects in space. The greater the distance to an object, the smaller the mass of the object appears.

Mass=1/distance

We therefore cannot tell whether a singular object, an object in space all on its own, is far away or if it just small. From our point of view it could be either one. We need a third object to reference. For example, if we look at a row of telephone poles, we assume that they are all the same size and get increasingly farther away in the distance.

With enough objects in space that relate to each others’ masses and distances, we get a group. With a group of objects, we can know how mass and distance relate among all the objects. Each telephone pole’s top and bottom are parallel and converge on a vanishing point. The objects’ size from our point of view is a linear relationship. The perceived distance between poles is D=x-1 where x is the length of the previous distance between the closer poles. The length of the entire perceived row of poles is the sum of each space: L=∑(x+1)/I where i is the distance between you and the first pole.

Harmonic Series Gives Form

 
 
But what about a group of randomly placed objects? Imagine that we place telephone poles in our scene at random. After a while, there will be so many poles that you can’t see through to the other side–all you see is telephone poles. The point at which this happens is the very instant your brain considers this group of telephone poles an object itself, a single unit of stuff.

At what point does this occur?

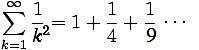It depends on the distance between the poles and the size of the poles. We use calculus. In mathematics, we use the harmonic series to tell us at what rate you can add smaller pieces of a pie to make the entire pie. Using the harmonic series, we know that the moment the field telephone poles become too dense to see through, all the poles a distance of 1 away from you add up to a mass of 1/4. All the poles a distance of 2 will add up to a mass of 1/9. And so forth. If you keep going, all the poles in the entire field add up to a mass of 1.

It is a very simple rate: 1/k². The poles look smaller at a linear rate, remember, as they get farther away. But 1/k² is the rate at which the poles appear to make up an overall object. This is also the rate at which light gets dimmer through space.

Haromic Series & Linear Series Prove Golden Mean

 
 
What happens when we make these two equations equal to each other: 1/x² = 1/(x+1)?

We will see the linear reduction of size for each telephone pole. We will also see the moment each telephone pole makes up an overall object. The rate at which mass gets smaller in distance is now equal to the rate at which smaller parts make up a whole. There is only one number that x can equal: 1.618 or the golden ratio. The golden ratio gives a relationship between distance and mass that lets the viewer determine if objects are either small or far away. If the objects fit into this proportion there is no question, because we can see how it fits into the overall group.

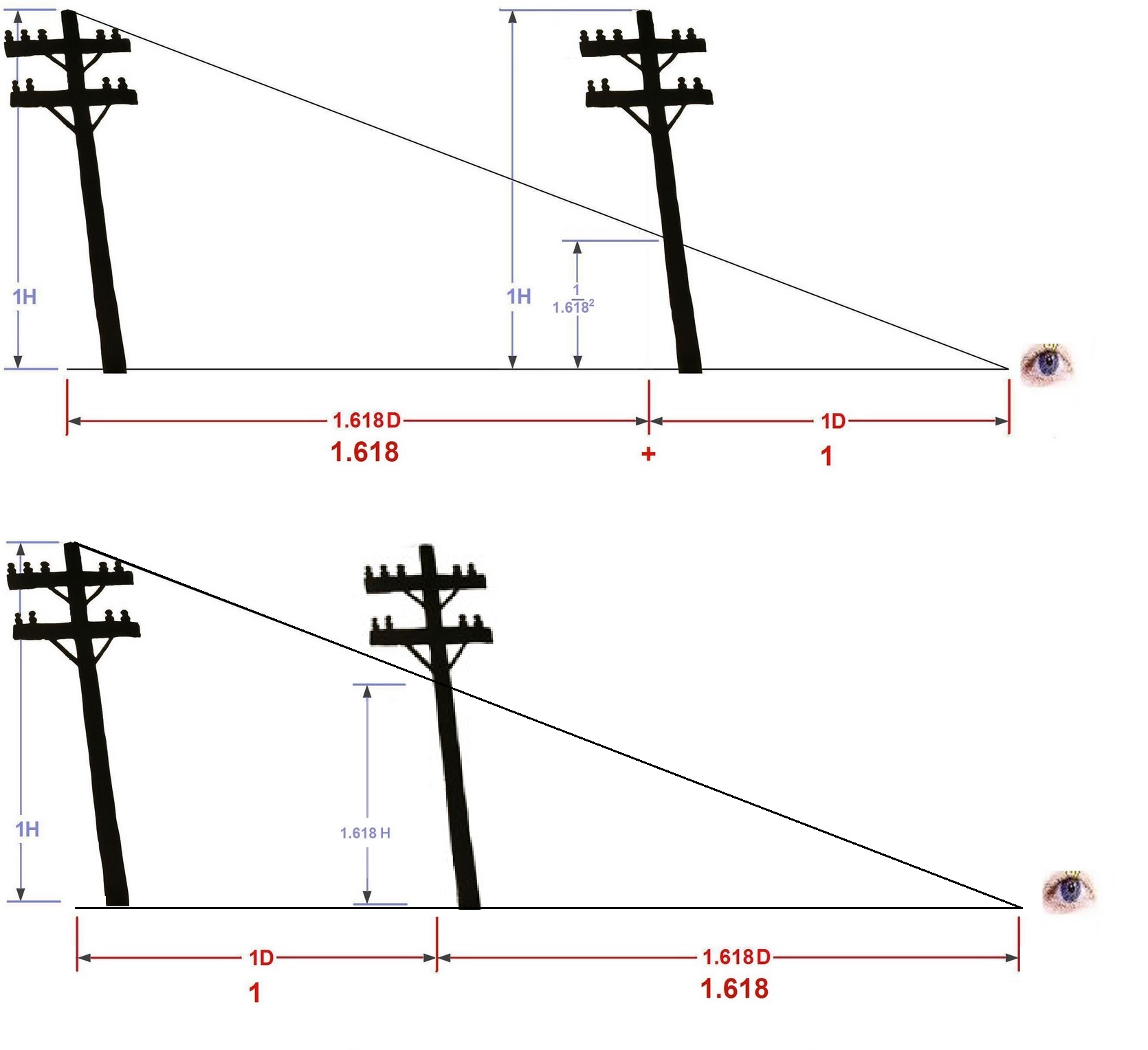
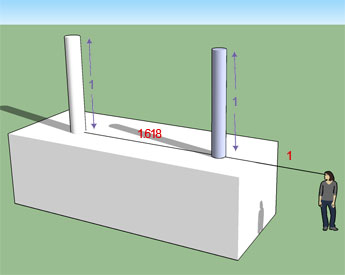
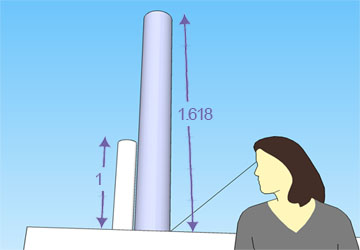
We can also demonstrate this geometrically. If the viewer is a distance of 1 away from the first telephone pole and the pole is 1 in size, all you need to do is space the second pole 1.618 away and it will appear to you 1/1.618 in size. Or you can make the second pole 1.618 in size, space it 1 away, and it will appear 1 in size. Or the viewer can be 1.618 away from the first pole and the second pole will appear 1.618 the size of the first pole.

The size that we see the second pole in proportionate to the distance between the objects and viewer. Going back to the Fibonacci sequence, the distance of time between reproductive events in a population is likewise proportionate to the size of the overall population.

Quantum Relationship Of Golden Proportions

 
 
An important idea in Quantum theory is that there is a definite size that relates all energy in the universe. You can reduce all matter to a smallest size, and then reduce it no smaller.

In our original problem of things getting smaller as distance, we therefore know that there is a point at which it appears the smallest possible. On the smallest scale possible, energy is made up of the same units. The distance between these units has a Golden Proportion relationship to the size of the units. This is the most fundamental basis of space in our universe. We know the speed of light determines time, therefore this relationship furthermore binds matter and time. The time it takes light to travel between groups of objects has a Golden Ration proportion to the size of the objects.

Think of the telephone poles as quantum units of energy, and think of distance as the momentum that separates those energies from the observer.

Parmenides contended that space doesn’t really exist if there is nothing in it and that motion or multiplicity therefore doesn’t exist. But it is the ability for energy to travel between states that determines what space is like. The golden mean is a standard how that space appears, according to the mass of the energies being perceived.

© Benjamin Blankenbehler 2012